平方和公式是计算公式,是连续自然数的平方和公式。
 证法一 (归纳猜想法): 1、N=1时,1=1(1+1)(2×1+1)/6=1 2、N=2时,1+4=2(2+1)(2×2+1)/6=5 3、设N=x时,公式成立,即1+4+9+…+x²=x(x+1)(2x+1)/6 则当N=x+1时, 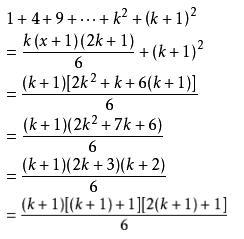 也满足公式。 根据数学归纳法,对一切自然数n有↓  成立。 证法二(利用恒等式↓)  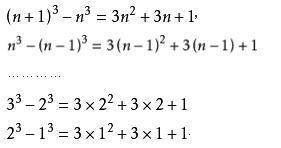 把这n个等式两端分别相加,得:  由于1+2+3...+n=n(n+1)/2 代入上式得:  整理后得: 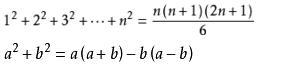 |
平方和公式是计算公式,是连续自然数的平方和公式。
 证法一 (归纳猜想法): 1、N=1时,1=1(1+1)(2×1+1)/6=1 2、N=2时,1+4=2(2+1)(2×2+1)/6=5 3、设N=x时,公式成立,即1+4+9+…+x²=x(x+1)(2x+1)/6 则当N=x+1时, 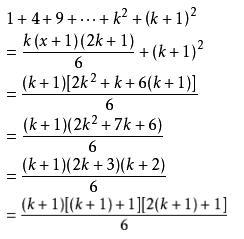 也满足公式。 根据数学归纳法,对一切自然数n有↓  成立。 证法二(利用恒等式↓)  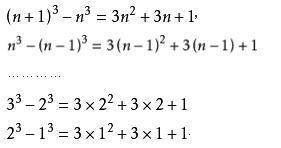 把这n个等式两端分别相加,得:  由于1+2+3...+n=n(n+1)/2 代入上式得:  整理后得: 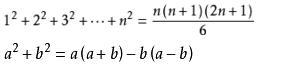 |