知识点总结：高中数学集合与常用逻辑用语

网络资源 发表于2023-10-12 14:27:30

知识点1  集合与元素

1、集合元素的三个特性：确定性、互异性、无序性；

2、元素与集合的关系：属于或不属于，用符号或表示

3、集合的表示法：列举法、描述法、图示法

4、常见数集的记法与关系图

知识点2  集合间的基本关系

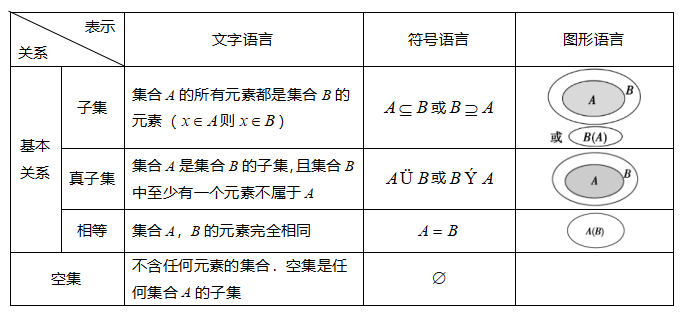
知识点3  集合的基本运算

1、集合交并补运算的表示

2、集合运算中的常用二级结论

（1）并集的性质：A∪∅＝A；A∪A＝A；A∪B＝B∪A；A∪B＝A⇔B⊆A.

（2）交集的性质：A∩∅＝∅；A∩A＝A；A∩B＝B∩A；A∩B＝A⇔A⊆B.

（3）补集的性质：A∪(∁UA)＝U；A∩(∁UA)＝∅．∁U(∁UA)＝A；∁U(A∪B)＝(∁UA)∩(∁UB)；∁U(A∩B)＝(∁UA)∪(∁UB)．

知识点4  充分条件与必要条件

1、充分条件与必要条件

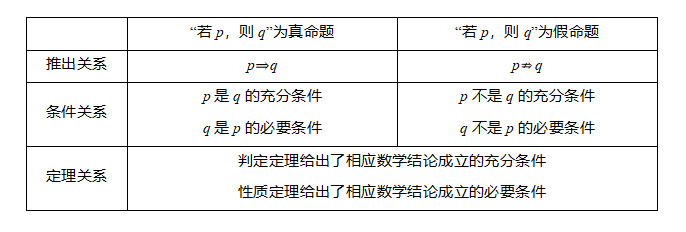
2、充要条件

（1）充要条件的定义

如果“若，则”和它的逆命题“若，则”均为真命题，即既有，又有，就记作。

此时，既是的充分条件，也是的必要条件，我们说是的充分必要条件，简称充要条件。

（2）充要条件的含义

若是的充要条件，则也是的充要条件，虽然本质上是一样的，但在说法上还是不同的，因为这两个命题的条件与结论不同。

（3）充要条件的等价说法：是的充要条件又常说成是成立当且仅当成立，或与等价。

知识点5  全称量词与存在量词

1、全称量词与全称量词命题

（1）全称量词：短语“所有的”“任意一个”在逻辑中通常叫作全称量词，并用符号“”表示．

【注意】

（1）全称量词的数量可能是有限的，也可能是无限的，由有题目而定；

（2）常见的全称量词还有“一切”、“任给”等，相应的词语是“都”

（3）全称量词命题：含有全称量词的命题，称为全称量词命题．

【注意】

（1）从集合的观点看，全称量词命题是陈述某集合中所有元素都具有某种性质的命题；

（2）一个全称量词命题可以包含多个变量；

（3）有些全称量词命题中的全称量词是省略的，理解时需要把它补出来。

如：命题“平行四边形对角线互相平行”理解为“所有平行四边形对角线都互相平行”。

2、存在量词与存在量词命题

（1）存在量词：短语“存在一个”“至少有一个”在逻辑中通常叫作存在量词，并用符号“”表示．

【注意】常见的存在量词还有“有些”、“有一个”、“对某些”、“有的”等；

（2）存在量词命题：含有存在量词的命题，叫作存在量词命题。

【注意】

（1）从集合的观点看，存在量词命题是陈述某集合中有一些元素具有某种性质的命题；

（2）一个存在量词命题可以包含多个变量；

（3）有些命题虽然没有写出存在量词，但其意义具备“存在”、“有一个”等特征都是存在量词命题

3、命题的否定：对命题p加以否定，得到一个新的命题，记作“”，读作“非p”或p的否定．

常见正面词语的否定：